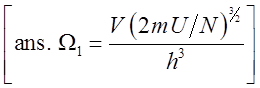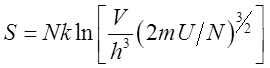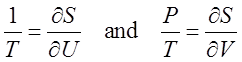Chaion Analytics

Entropy in Statistical Mechanics

Copyright ï³°an> 2011 by Robert Finkel

Statistical Mechanics Home

ã°¡n style="font:7.0pt "Times New Roman"">       Probabilities

ã°¡n style="font:7.0pt "Times New Roman"">       Averaging

ã°¡n style="font:7.0pt "Times New Roman"">       Entropy

ã°¡n style="font:7.0pt "Times New Roman"">       Moles & Gas Constant

ã°¡n style="font:7.0pt "Times New Roman"">       Thermodynamics

ã°¡n style="font:7.0pt "Times New Roman"">       Partition Function

ã°¡n style="font:7.0pt "Times New Roman"">       Gibbs Entropy

CONTACT

Copyright ï³°an> 2011 by Robert Finkel

Why Entropy?

Entropy is intimately connected to statistical concepts and is often one of the functions most readily found from molecular models. Entropy S appears in the fundamental thermodynamic expression (see Thermodynamics) and can be connected to any and all of the more familiar thermodynamic functions like energy or pressure.

Three forms of entropy are widely used in thermal physics. The thermodynamic or classical form is where is an increment of heat added reversibly to a system. (Reversibility is the thermal analog of ideal frictionless motion in mechanics.) A second form is Boltzmann entropy--a foundation of statistical mechanics--as it is intimately related to the randomness of a system; it is presented on this page. We consider a third form on the Gibbs Entropy page. The three forms are virtually equivalent and the best choice can depend on the application.

Boltzmann Entropy

Most traditional presentations of statistical mechanics begin by expressing entropy in terms of W, the number of equally probable microscopic states that constitute a given macroscopic state. For example, a ᣲoscopic㴡te where 2 people (molecules) are seated in any 6 chairs can be achieved in W = 30 飲oscopicꠠways.

Entropy is a technical measure of randomness and this is apparent in the statistical form. The entropy is called the Boltzmann entropy. Ludwig Boltzmann hanged himself in 1906 in a bout of depression. His entropy equation is engraved on his tombstone. It can be regarded as the defining entropy expression.

Our objective on this page is to use Eq.(1) to derive state equations for ideal gas. A thermodynamic state equation like the familiaris a macroscopic description of a system that depends only on the current state of the system, not on the history by which the system arrived at that state. Toward this end, we briefly review the concept of matter waves.

Review of Matter Waves

De Broglie recognized that all matter exhibits both wave and particle properties. The expression deduced by de Broglie applies to all matter including the most familiar particles; photons, electrons, protons, and neutrons. Each object is both a particle and a wave and shows one property or the other depending upon the circumstances. De Broglie expressed the wavelength l of the matter-wave in terms of the momentum p of the particle. Wavelength is Planck's constant h divided by p,.

You can use this derive some approximate expressions for the number of microstates W in an ideal gas. While these are approximate, they enable us to derive some correct state equations. This can be attributed to the fact that unimportant approximate particulars are washed out by the averaging process while the salient features survive to be reflected in the macroworld.

Ideal Gas Microstates

A crude measure of the number of microstates, denoted , available to a single molecule of ideal gas in a volume V uses the idea that each particle occupies a cube of volume where the sides are one de Broglie wavelength l. The number of ways one particle can fit in V is then V/l³ so .We will want to express entropy in terms of energy U and volume V so the expression must be manipulated using and the average individual energy of a free particle given by where m is the particle mass. (Check that kinetic energy is .)

ã°¡n style='font:7.0pt "Times New Roman"'>       Evaluate microstates for one particle of a monatomic ideal gas in volume V using the (crude) idea that each particle occupies a cube of volume l³ where the sides are one de Broglie wavelength l. Express your result in terms of U and V.

The total number of microstates for N particles is the product of the of all the independent individual microstates, . The system entropy then follows from the Boltzmann expression. The final result is

This is not pretty, but it is easy to extract from it all possible macroscopic information regarding ideal gas. We do this with equations from thermodynamics involving partial derivatives.

Partial Derivatives

Consider a function S that depends on more than one independent variable, say V and U. We often need to differentiate S with respect to one variable, say V, while treating any other independent variables (like U) as if they are constants. This is the partial derivative of S with respect to V and is denoted as

.

ã°¡n style='font:7.0pt "Times New Roman"'>       Given a function , find and

      [ans. ]

Ideal Gas

Ideal gas derivations are favorites to illustrate applications of statistical mechanics. Two useful thermodynamic equations are developed in our Thermodynamics page. Here I present them as given:

ã°¡n style='font:7.0pt "Times New Roman"'>       Apply the thermodynamic equations above to the entropy to find the state equations and

Go to Thermodynamics