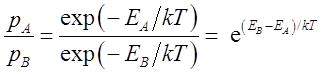|
Chaion Analytics |
Probabilities in Statistical MechanicsCopyright ï³°an> 2011 by Robert Finkel |
|||||
|
Canonical
Probabilities One of the most important expressions
in statistical mechanics is the canonical distribution; an expression for the probability pj that a particle or system is in an
energy level Ej selected from a
list of possible energies E1,
E2,..
This canonical distribution is also termed the Boltzmann distribution. Here is the basic form
where k is the Boltzmann
constant (
The
sum is over all the possible energies.
Equation (1) is a central result in statistical mechanics and we defer
a derivation of this important equation to textbooks. ã°¡n
style='font:7.0pt "Times New Roman"'> Show that Consider a molecule
that can have two isomeric states A and B with corresponding energies
The fraction of
molecules in state A is
Notice that the We can often 塤ê a result like this without inserting a single number. The result tells us
that when the energy in the B-state is higher than that of the A-state, the
population of A is greater to maintain equilibrium. Furthermore, when the
temperature is very high the exponent is small and the populations tend to
approach each other. 㰡n style='font:7.0pt "Times New Roman"'> Isomer A has energy kT and isomer B has energy 0.31kT. Calculate the probability of the molecule to be in state A. [ans. 0.33] Gas Constant and Boltzmannïnstant The expressions on this page use the Boltzmann constant k most often preferred by physicists while chemists and biologists most prefer using the universal gas constant R for these same expressions. Equations (1) and (2) retain their form with k replaced by R. Then energies are energies per mole rather than energies per particle. A simple relation between the two is found in these pages: Moles and the Gas Constant.
Go to Averaging
|

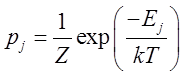
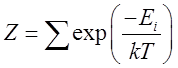 .
.